Расчет доходности облигаций в excel

Поиск на сайте

Простая доходность облигации — это доходность, рассчитанная в %годовых и зависящая от суммы купонного дохода по облигации и разницы в стоимости самой облигации в моменты покупки и продажи. От эффективной доходности отличается тем, что в расчёт не принимается возможность реинвестирования полученного купонного дохода в данную облигацию.

Считаю, что простую доходность облигации уместно использовать, если выбранный срок инвестирования в облигацию невысок (например, до 2 лет) и сумма инвестирования невелика. В таком случае полученного купонного дохода просто не хватит для реинвестирования, и эффективную доходность считать нет смысла.

В данном примере разберём расчёт простой доходности облигации к погашению на примере одной из популярных государственных облигаций (ОФЗ) ОФЗ-26218-ПД. Расчёт других облигаций (муниципальных и корпоративных) ничем принципиально не отличается от расчёта доходности ОФЗ.

Пример представлен для случая покупки ОФЗ через брокерскую контору, принцип расчёта доходности так называемых «народных ОФЗ«, приобретаемых через банки, немного другой (есть дополнительные комиссии и условия досрочного возврата) и будет рассмотрен отдельно.

Для расчёта необходимо знать следующие данные:

• номинал облигации (с учётом прошедшей амортизации),
• дату погашения облигации (в этом простом примере не будем рассматривать доходность к оферте),
• ставка купонов (в % годовых),
• сколько купонов в год выплачивается (при равномерной выплате),
• дату последнего выплаченного купона,
• текущая рыночная цена (в % от номинала).

Всю эту информацию можно найти на специализированных сайтах типа rusbonds.ru, cbonds.info, bonds.finam.ru и многих других.

Итак, расчёт простой доходности облигации к погашению ОФЗ-26218-ПД. Это облигация подходит для простого расчёта, так как есть постоянная доходность (размер купона не меняется) и нет амортизации (то есть номинал неизменен). Для случаев амортизируемых облигаций и переменных купонов лучше использовать другие способы, которые рассмотрим отдельно.

В первых строках размещена общая информация об облигации. В ячейке С7 рассчитывается срок до погашения простой формулой «=C6-СЕГОДНЯ()«.

Обратите внимание, что пример сохранён 25.05.2017, в другой день все расчёты будут иными.

В строке 11 рассчитывается число купонов для погашения формулой «=ОКРУГЛВНИЗ(C7/365;0)*C10+1«: вычисляем количество полных лет до погашения, умножаем на количество купонов в год и добавляем 1 (так как последний купон выплачивается в момент погашения).

В строке 13 рассчитывается накопленный купонный доход (НКД) формулой «=(СЕГОДНЯ()-C12)/365*C9*C5«: он зависит от текущей даты, даты последней выплаты купона, купонной доходности и номинала.

С помощью рассчитанного НКД и цены, по которой облигация торгуется на рынке («чистой цены»), рассчитывается так называемая «грязная цена» — стоимость, которую необходимо заплатить за покупку облигации (без учёта брокерских комиссий). Это сумма инвестиций.

В строках 17-20 рассчитывается доход от инвестирования в облигацию ОФЗ, равный доходу от погашения облигации плюс купонный доход за всё время инвестирования.

В строке 22 рассчитана прибыль, равная разности дохода и сумме инвестиций. В строке 23 — она же в процентном виде. Видим, что за время инвестирования сумма инвестиций более чем удвоилась, но срок очень долгий (14 лет) и простая доходность к погашению составила всего лишь 7,35%.

Эту таблицу можно использовать для расчёта простой доходности к погашению любых облигаций, которые имеют фиксированный купон и не предусматривают амортизацию номинала. Для более сложных случаев стоит составить таблицу платежей и поступлений (финансовых потоков) и использовать функцию Excel ЧИСТВНДОХ, как это сделано в следующем примере расчёта эффективной доходности облигации ОФЗ, смотрите соответствующую статью Расчёт эффективной доходности облигации к погашению.

Скачать пример расчёта простой доходности облигации ОФЗ к погашению : doh_obl_prost

Финансовые показатели облигаций могут быстро рассчитываться в Excel. Для этого используется функция ДОХОД. С ее помощью вычисляется доходность ценных бумаг, по которым периодически выплачиваются проценты (дивиденды).

Как работает функция ДОХОД в Excel?

Облигации – это финансовый инструмент. Предприятие, выпустившее облигации, выступает в роли заемщика. Нуждаясь в привлечении средств, оно выпускает и выбрасывает на рынок такие ценные бумаги. Покупатель облигаций, фактически, является заимодавцем. Ставка купона – это процент, который получает покупатель облигации за то, что предоставил свои средства в пользование.

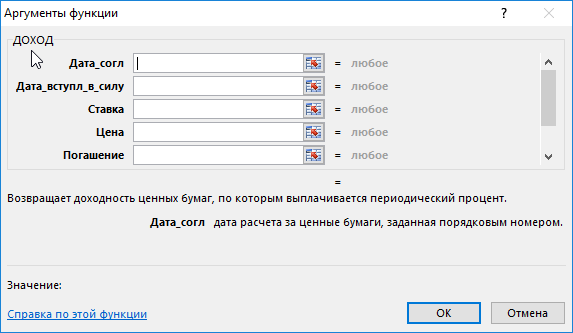
Как рассчитать доходность облигаций в Excel? Для решения данной задачи используется функция ДОХОД. Как и любая другая функция, ее синтаксис состоит из имени и аргументов. В строке формул сначала ставится знак равенства, после прописывается имя функции, а затем заполняем ее аргументы входящими значениями всех необходимых показателей.

Всего аргументов у сложной функции 7. Из них 6 обязательных для заполнения:

1. Дата_согл. Расчетный день, когда облигация продана. Дата, когда долговые обязательства переданы покупателю. Не стоит путать ее с датой выпуска облигации.
2. Дата_вступл_в_силу. День, когда заем возвращается покупателю. Это срок погашения облигации, когда истекает срок ее действия.
3. Ставка. Годовая ставка процентов по облигации. Процент, который получает покупатель ценных бумаг.
4. Цена. Показатель определяет цену облигации на 100 рублей номинала.
5. Погашение. Стоимость, по которой выкупаются ценные бумаги.
6. Частота. Число выплат по облигации в год. Может быть равна 1, 2 или 4.
7. Базис. Этот аргумент не является обязательным. Поэтому он заключается в квадратные скобки. Он определяет способ вычисления дней.

Существует 5 видов базиса:

• — 0 – Американский 30/360;
• — 1 – факт/факт;
• — 2 – факт/360;
• — 3 – факт/365;
• — 4 – Европейский 30/360.

Аргументы всегда берутся в круглые скобки. Все они перечисляются по порядку. Между ними ставится знак «;».

Синтаксис функции прописывается следующим образом:

=ДОХОД(дата_согл; дата_вступл_в_силу; ставка; цена; погашение; частота; [базис])

Обязательно учитывать то, что все даты в Excel записываются в виде последовательных чисел. Недопустимо использование текстового формата. За 1 принято 1 января 1900 года. Все последующие даты просто прибавляют число прошедших дней. Поэтому все значения рассчитываются с помощью функции «ДАТА».

Результатом применения функции является определение прибыльности облигаций. Программа может выдать не результат, а знак ошибки #ЧИСЛО! Это происходит в нескольких случаях:

• введены даты без использования функции «ДАТА»;
• значение ставки меньше нуля;
• указана цена меньше или равная нулю;
• погашение указано меньше или равно нулю;
• базис меньше нуля или больше четырех.

Примеры использования функции ДОХОД для анализа облигаций

Для вычисления доходности ценных бумаг нужно ввести в первый столбик таблицы все аргументы функции.

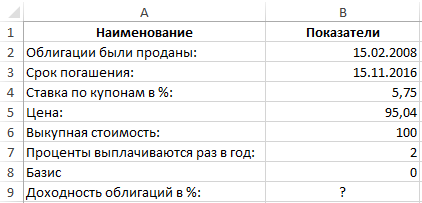
Пример 1. Необходимо вычислить доходность облигаций при следующих условиях:

1. Облигации были проданы 15 февраля 2008 года.
2. Срок погашения – 15 ноября 2016.
3. Ставка по купонам определена 5,75%.
4. Цена составляет 95.04 номиналов.
5. Выкупная стоимость — 100 номиналов.
6. Проценты выплачиваются раз в полгода.
7. Значение базиса – 0 (30/360).

Последовательно вводите все значения заполняя таблицу с данными:

В ячейку B9 вводите данные для аргументов функции ДОХОД. Формула будет выглядеть так:

Доходность облигаций составляет 4,26%.

Можно вводить формулу с клавиатуры или указывать соответствующие ячейки мышью. При этом прописать имя функции нужно вручную. Затем откройте скобку и последовательно через «пробел» укажите все ячейки, которые должны быть учтены.

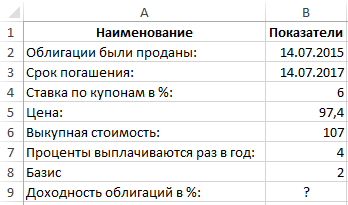
Пример 2. Предприятие продало облигации 14 июля 2015. Установлен небольшой срок их погашения 14 июля 2017. Предлагается ставка 6%. Цена бумаг 97,4 номинальных значений. Стоимость для выкупа – 107 номиналов. Выплата процентов проводится 4 раза в год. Базис 2 – (48/360).

Для вычисления прибыльности облигации введите данные в таблицу по принципу, который стал понятен из примера 1:

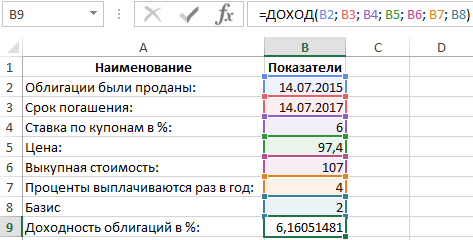
В итоговой ячейке B9 приписываем функцию:

Это обозначает, что расчет доходности к погашению облигаций составляет (6,16% х 2года)=12,32%.

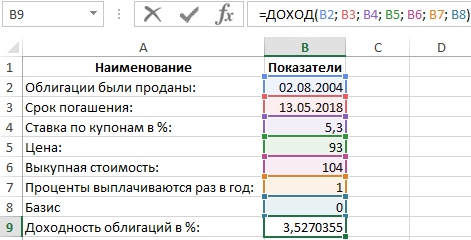
Пример 3. Ценные бумаги проданы 2 августа 2004. Погашение произошло 13 мая 2018. Купонная ставка по ним – 5,3%. Цена бумаг – 93 номинала. Стоимость для выкупа – 104 номинала. Проценты начисляются раз в год. Базис – 0 (30/360).

По аналогии составляем таблицу, используя функцию =ДОХОД():

Прибыльность акций оценена в 3,52%.

С помощью программы Excel удалось всего за несколько минут установить, что самыми прибыльными инвестициями являются облигации из второго примера.

3.2 Анализ краткосрочных бескупонных облигаций

Как уже отмечалось в предыдущей главе, бескупонные облигации – это дисконтные ценные бумаги, которые размещаются ниже номинала.

В разное время отечественный рынок краткосрочных бескупонных облигаций был представлен государственными, республиканскими (субъектов федерации) и муниципальными ценными бумагами, со сроками обращения 3, 6, 9 и 12 месяцев. При этом наиболее надежными, ликвидными и безрисковыми считаются ценные бумаги, представляющие собой краткосрочный государственный долг , т.е. долг правительства юридическим и физическим лицам. Кроме того, в большинстве стран инвестиции в государственные обязательства предполагают получение различных налоговых льгот.

Характерными примерами подобных ценных бумаг являются трехмесячные казначейские векселя (treasury bills) федерального правительства США и государственные краткосрочные обязательства России (ГКО), выпускаемые в бездокументарной форме.

3.2.1 Доходность краткосрочных бескупонных облигаций

Поскольку бескупонные облигации всегда реализуются с дисконтом, норма доходности, которую получит инвестор, зависит от разницы между уплаченной ценой (ценой покупки – Р ) и номиналом N (ценой погашения). Так как номинал облигации всегда известен (или может быть принят за 100%), для определения доходности операции достаточно знать две величины – цену покупки P (либо курс К ) на дату проведения операции и срок до погашения в днях – t .

Доходность краткосрочного обязательства – Y

Как правило, расчет доходности краткосрочных облигаций осуществляется по формуле простых процентов в виде годовой ставки Y . В этом случае, формула для определения доходности краткосрочного обязательства может иметь следующий вид:

, (3.16)

где t – число дней до погашения; Р – цена покупки; N – номинал; К – курсовая стоимость; В = <360, 365 или 366>– используемая временная база (360 для обыкновенных процентов; 365 или 366 для точных процентов).

Краткосрочное обязательство со сроком погашения 90 дней было приобретено по цене 98,22 от номинала. Определить доходность операции для инвестора:

а) с использованием обыкновенных процентов

, или 7,2%

б) с использованием точных процентов

, или 7,22%.

В зарубежной практике рассчитываемый по формуле (3.16) показатель Y также часто называют эквивалентным купонным доходом . Как следует из названия, этот показатель представляет собой годовую купонную ставку по долгосрочной облигации, соответствующую доходности краткосрочного обязательства.

Доходность краткосрочного обязательства к погашению Y можно также рассматривать в качестве цены займа для его эмитента. Таким образом, стоимость заемных средств для государственной казны в примере 3.1 составит 7,22% (7,2%).

Как уже отмечалось, для государственных краткосрочных обязательств могут быть предусмотрены различные налоговые льготы.

Это важнейшее обстоятельство учитывает формула доходности ГКО к погашению, рассчитываемая по официальной методике ЦБР :

, (3.17)

где P – средневзвешенная цена аукциона (либо цена закрытия, т.е. последняя цена сделки на торгах); Т – условная ставка налога .

Вычисленная по методике ЦБР доходность к погашению обязательства из предыдущего примера составит:

0,722 ´ 1 / (1 — 0,35) = 0,096 или 9,6%.

Включение с мая 1993 года налоговых льгот в расчет доходности ГКО играло роль своеобразной рекламы и было призвано привлечь внимание инвесторов к молодому и неокрепшему на тот момент рынку облигаций. В настоящее время этот показатель в значительной мере утратил свое значение и представляет ценность лишь как экономический индикатор, характеризующий взаимосвязь между состоянием рынка государственных ценных бумаг и процентными ставками по межбанковским кредитам (МБК).

Следует отметить, что рассчитываемые по формулам (3.16 – 3.17) показатели имеют, по крайней мере, два недостатка:

не могут быть использованы для сравнения эффективности проведения краткосрочных операций с другими видами инвестиций, в т.ч. – долгосрочными;

не учитывают возможность неоднократного реинвестирования полученных доходов в течении года, возникающую при проведении операций с некоторыми видами краткосрочных обязательств (например – 3-х или 6 месячными ГКО и др.).

Для преодоления указанных ограничений используют более универсальный показатель – эффективная доходность.

Эффективная доходность краткосрочного обязательства – YTM

В случае возможности неоднократного реинвестирования полученных доходов возникает необходимость в использовании показателя, адекватно отражающего общую эффективность проводимых операций. Очевидно, что более корректно предположение о многократном реинвестировании учитывает формула наращения по сложным процентам.

В этой связи для расчета доходности краткосрочного обязательства может быть использована следующая формула:

, (3.18)

где t – число дней до погашения; Р – цена покупки; N – номинал; В = <360, 365 или 366>– используемая временная база.

Осуществим расчет доходности YTM для краткосрочного обязательства из примера 3.1:

YTM = (100 / 98,22) 365/90 -1 = 0,075 или 7,5%.

В отечественной практике данный показатель получил название эффективной доходности . В публикуемых финансовых сводках и аналитических обзорах для его обозначения используется принятая во всем мире и уже знакомая нам по прошлой главе аббревиатура YTM (yield to maturity) .

Рассчитываемый по формуле сложных процентов, показатель YTM может быть использован для сравнения эффективности проводимых операций с ценными бумагами, имеющими различные сроки погашения.

В случае, если краткосрочная бескупонная облигация приобретается с целью последующей реализации (т.е. для проведения арбитражных операций), ее доходность определяется ценами и сроками купли-продажи:

, (3.19)

, (3.20)

где P 1 – цена покупки в момент t = 1; P 2 – цена перепродажи в момент t = 2; t 1 – число дней до погашения в момент покупки; t 2 – число дней до погашения в момент перепродажи.

3.2.2 Оценка стоимости краткосрочных бескупонных облигаций

Процесс оценки стоимости краткосрочной бескупонной облигации заключается в определении современной величины элементарного потока платежей по формуле простых процентов, исходя из требуемой нормы доходности (рыночной ставки) Y .

С учетом используемых обозначений, формула текущей стоимости (цены) подобного обязательства будет иметь следующий вид:

. (3.21)

Поскольку номинал бескупонной облигации принимается за 100%, ее курсовая стоимость равна:

. (3.22)

Какую цену заплатит инвестор за бескупонную облигацию с номиналом в 100,00 и погашением через 90 дней, если требуемая норма доходности равна 12%?

100 / (1 + 0,12 ´ 90/365) = 97,12.

Из приведенных соотношений следует, что фундаментальные взаимосвязи между ценой и доходностью, рассмотренные в предыдущей главе, справедливы и для краткосрочных облигаций. Таким образом, цена краткосрочного обязательства Р связана обратной зависимостью с рыночной ставкой (нормой доходности) Y и сроком до погашения t .

В случае, если бумага приобретается для проведения арбитражных операций, цена сделки P 2 , обеспечивающая получение требуемой нормы доходности Y , определяется из следующего соотношения:

, (3.23)

где P 1 – цена покупки в момент t = 1; t 1 – число дней до погашения в момент покупки; t 2 – число дней до погашения в момент перепродажи.

3.2.3 Автоматизация анализа краткосрочных бескупонных облигаций

Для автоматизации анализа краткосрочных облигаций в ППП EXCEL реализована специальная группа из 6 функций (табл. 3.1). Все функции данной группы являются дополнительными.

Таблица 3.1
Функции для анализа краткосрочных финансовых операций.

Наименование функции

Формат функции

Англоязычная версия

Русифицированная
версия

TBILLYIELD

ДОХОДКЧЕК

ДОХОДКЧЕК(дата_согл; дата_вступл_в_силу; цена)

TBILLPRICE

ЦЕНАКЧЕК

ЦЕНАКЧЕК(дата_согл; дата_вступл_в_силу; скидка)

TBILLEQ

РАВНОКЧЕК

РАВНОКЧЕК(дата_согл; дата_вступл_в_силу; скидка)

СКИДКА

СКИДКА(дата_согл; дата_вступл_в_силу; цена; погашение; [базис])

YIELDDISC

ДОХОДСКИДКА

ДОХОДСКИДКА(дата_согл; дата_вступл_в_силу; цена; погашение; [базис])

PRICEDISC

ЦЕНАСКИДКА

ЦЕНАСКИДКА(дата_согл; дата_вступл_в_силу; скидка; погашение; [базис])

Первые 4 функции этой группы исторически были реализованы для удобства проведения расчетов по операциям с краткосрочными казначейскими векселями правительства США. Функции используют следующие аргументы:

дата_согл – дата приобретения облигаций (дата сделки);

дата_вступл_в_силу – дата погашения облигации;

цена – цена покупки (в % к номиналу);

погашение – цена погашения (100 % от номинала);

скидка – эквивалентная доходности учетная ставка d ;

базис – временная база.

Последний аргумент " базис " не является обязательным, однако играет важнейшее значение, так как определяет временную базу и оказывает непосредственное влияние на точность вычислений. Список допустимых значений аргумента и соответствующие пояснения приведены в табл. 3.2.

Таблица 3.2
Допустимые значения аргумента " базис "

Значение

Тип начисления

US (NASD) 30/360

Фактический/фактический

Фактический/360

Фактический/365

Европейский 30/360

В российской практике аналогичными ценными бумагами являются государственные краткосрочные обязательства (ГКО). Однако проблема использования функций ДОХОДКЧЕК() и ЦЕНАКЧЕК() для анализа отечественных краткосрочных облигаций заключается в том, что в реализуемых ими формулах за временную базу принят обыкновенный или финансовый год (360 дней в году, 30 дней в месяце) тогда как в российской практике (в том числе, в официальных методиках ЦБР и МФ РФ) применяют точное число дней в году и в месяце (365/365).

Поскольку продолжительность подобных операций не превышает 360 дней, данная проблема решается достаточно простым путем – корректировкой полученных результатов на поправочные коэффициенты q = 365/360 и v = 360/365.

Продемонстрируем технику использования данных функций и обхода указанных выше проблем на примере, взятом из реальной практики отечественного рынка государственных краткосрочных облигаций (ГКО) .

Рассматривается возможность приобретения 3-х месячных ГКО серии N 21072. Средневзвешенная цена на 18/03/97 – 93,72. Дата погашения – 28/05/97 . Провести анализ этой операции.

Подготовьте ЭТ с исходными данными примера, как показано на рис. 3.1.

Рис. 3.1. ЭТ с исходными данными примера

Формулы для расчета поправочных множителей q и v в ячейках D5 и D6 имеют следующий вид:

Приступим к разработке шаблона для анализа краткосрочных бескупонных облигаций с использованием функций ДОХОДКЧЕК() , ЦЕНАКЧЕК() , СКИДКА() , РАВНОКЧЕК() .

Функция ДОХОДКЧЕК(дата_согл; дата_вступл_в_силу; цена)

Функция ДОХОДКЧЕК() вычисляет доходность облигации к погашению по простым процентам , т.е. величину Y. Однако как уже отмечалось, осуществляемый ею расчет предполагает использование обыкновенных, в отличие от принятых в отечественной практике точных процентов. Обход данной проблемы заключается в корректировке полученного результата на величину q = 365/360, рассчитанную в ячейке D5. С учетом вышеизложенного, формула, заданная в ячейке В13, будет иметь следующий вид:

=ДОХОДКЧЕК( В6; В7; В8) * D5 (Результат: 34,45%).

Определив величину Y мы можем легко рассчитать доходность операции по методике ЦБР, т.е. с учетом налоговых льгот:

Введите в ячейку B14: =B13*(1/(1-D8)) (Результат: 53,00%).

Функция СКИДКА() определяет величину учетной ставки d (ставки дисконта), соответствующей цене покупки облигации и эквивалентной ее доходности к погашению Y (ячейка В15):

=СКИДКА(B6;B7;B8;B9;D7) (Результат: 32,28%).

Отметим, что для получения точного результата здесь явно задан необязательный аргумент " базис " (ячейка D7), равный 3 (т.е. точное число дней по операции и фактическое число дней в году) . Возможность указания этого аргумента избавляет нас от необходимости вводить поправочные коэффициенты.

Обратите внимание также на то, что величина учетной (антисипатив-ной) ставки d меньше нормы доходности Y (декурсивной ставки).

Функция ЦЕНАКЧЕК(дата_согл; дата_вступл_в_силу; скидка)

Определив величину скидки (В15), мы можем легко вычислить курсовую цену облигации (ячейка B16):

=ЦЕНАКЧЕК(B6;B7;B15*D6) (Результат: 93,72).

Как и следовало ожидать, она равна цене покупке (т.е. средневзвешенной биржевой цене в данном случае). Обратите внимание на использование поправочного коэффициента v (ячейка D6) для корректировки величины скидки (ячейка В15). Необходимость подобной корректировки возникает вследствие разных временных баз, используемых при вычислении скидки (точные проценты) и цены (обыкновенные проценты), в силу алгоритма, реализуемого функцией ЦЕНАКЧЕК() .

Функция РАВНОКЧЕК(дата_согл; дата_вступл_в_силу; скидка)

Функция РАВНОКЧЕК() позволяет рассчитать показатель эквивалентного годового купонного дохода по известной величине ставки дисконта (ячейка В15). Этот показатель широко используется в практике США. Для нашего примера с учетом поправочного коэффициента v он будет равен (ячейка В17):

=РАВНОКЧЕК(B6;B7;B17*D6) (Результат: 34,45%).

Нетрудно заметить, что в случае использования точных процентов, возвращаемая функцией величина будет всегда равна доходности Y .

Вычисление эффективной доходности YTM осуществляется по сложным процентам , поэтому воспользоваться функциями для анализа краткосрочных финансовых операций для ее исчисления мы не можем.

Существуют два пути решения проблемы. Первый заключается в непосредственной реализации соотношения (3.18) средствами ППП EXCEL. С учетом размещения исходных данных, формула для вычисления YTM будет иметь следующий вид (ячейка В18):

=(B9/B8)^(365/(B7-B6)) -1 (Результат: 39,57%).

Второй способ основан на том, что эффективная доходность к погашению ценной бумаги представляет собой внутреннюю норму рентабельности данной инвестиции (т.е. показатель IRR ). Тогда для ее исчисления можно воспользоваться уже упоминавшейся в первой главе функция ЧИСТВНДОХ() , предварительно задав цену покупки в ячейке В8 со знаком минус (блок значений потока платежей согласно формату функции ЧИСТВНДОХ() должен начинаться с отрицательного числа, т.е. оттока средств):

=ЧИСТВНДОХ(B8.B9;B6.B7) (Результат: 39,57%).

Оба способа дают аналогичные результаты. Однако в случае использования функции ЧИСТВНДОХ() необходимо задавать цену покупки в ячейке В8 с отрицательным знаком, что в свою очередь приводит к необходимости указания данного аргумента со знаком минус в функциях ДОХОДКЧЕК() и СКИДКА() . С учетом вышеизложенного, для рассматриваемого способа вычисления YTM эти функции должны быть заданы в ячейках В13 и В15 следующим образом:

=СКИДКА(B6; B7; -B8; B9; D7) (Результат: 32,28%).

=ДОХОДКЧЕК( В6; В7; -В8) * D5 (Результат: 34,45%).

Вы можете выбрать любой способ расчета YTM , по своему усмотрению. Далее предполагается, что при формировании шаблона для расчета YTM в ячейке В18 было реализовано соотношение (3.18):

=(B9/B8)^(365/(B7-B6)) -1 (Результат: 39,57%).

Для полноты анализа в ячейке В19 рассчитано число дней, оставшихся до погашения ГКО этой серии, а в ячейке В20 – величина абсолютного дохода по данной операции.

Введите в ячейку В19: =В7-В6 (Результат: 71).

Введите в ячейку В20: =В9-В8 (Результат: 6,28).

Полученная в результате таблица должна соответствовать рис. 3.2.

Рис. 3.2. Решение примера 3.3

В табл. 3.3 приведен фрагмент итоговой сводки результатов сделок в системе единых межрегиональных торгов по ГКО за 18.03.97 г .

Таблица 3.3
Результаты торгов ГКО на 18.03.97