Средняя ожидаемая доходность формула

Ожидаемая доходность — средневзвешенный, наиболее ожидаемый доход финансового инструмента. Показатель ожидаемой доходности учитывает все возможные доходы и определяет весомость того дохода, получение которого имеет наибольшую вероятность. В основу ожидаемой доходности положено понятие математического ожидания.

Ожидаемая доходность вычисляется по формуле:

M ⁡ ( R ) = ∑ i = 1 n P i ∗ R i <displaystyle operatorname (R)=sum _^P_*R_> ,

P i <displaystyle P_> — вероятность получения доходности R i <displaystyle R_> ,

Например, если известно, что инвестиция даёт 50 % вероятности получения 10 % доходности, 25 % вероятности получения 20 % доходности, 25 % вероятности получения −10 % доходности, ожидаемая доходность будет равна 7,5 %

= (0,5) (0,1) + (0,25) (0,2) + (0,25) (-0,1) = 0,075 = 7,5 %

Фактическая доходность может отличаться от полученного значения ожидаемой доходности. Статистический метод вычисления дисперсии случайной величины позволяет измерить вероятность отклонения фактической доходности от ожидаемой доходности. Чем выше дисперсия доходности у финансового инструмента, тем больше неопределённость у инвестора о будущих доходах. Следовательно инструмент с большей величиной дисперсии доходности является более рискованным финансовым инструментом.

Дисперсия [ править | править код ]

Дисперсия случайной величины доходности вычисляется по формуле

σ 2 = ∑ i = 1 n ( R i − M ( R ) ) 2 P i <displaystyle <>sigma ^<2>=sum _^left(R_-M(R)
ight)^<2>P_>

Для приведённого выше примера дисперсия будет равна 0,011875:

= (0,1-0,075)² * (0,5) + (0,2-0,075)² * (0,25) + (-0,1-0,075)² * (0,25) = 0,011875

В сфере инвестирования ожидаемая доходность (англ. Expected Rate of Return) представляет собой процентную ставку или сумму, которую инвестор ожидает получить в течение определенного периода времени от вложений в определенный актив. С практической точки зрения этот показатель может быть рассчитан исходя из полного набора вероятностей, либо на основе исторических данных о доходности актива.

Формула

В случае, если заранее известен полный набор вероятностей, то есть вероятности всех возможных вариантов исхода событий, ожидаемую доходность можно рассчитать использовав следующую формулу:

(1)

где P_i – вероятность наступления i-го исхода событий;

k_i – доходность при i-ом исходе событий;

n – количество исходов событий.

В условиях реального финансового рынка инвестор, как правило, принимает решение на основании имеющейся информации об исторической доходности ценной бумаги. В этом случае ожидаемая доходность рассчитывается как среднеарифметическое:

(2)

k_i – доходность ценной бумаги в i-ом периоде;

n – количество наблюдений.

Пример расчета

Пример 1. Финансовый аналитик рассматривает возможность включения в портфель инвестора одной дополнительной акции, выбирая из трех компаний, работающих в сфере оптово-розничной торговли. При этом он рассматривает три возможных сценария развития событий, вероятность и предполагаемая доходность которых представлены в таблице.

Чтобы определить ожидаемую доходность каждой из ценных бумаг, необходимо воспользоваться первой из приведенных выше формулой. Для акций Компании А она составит 11,25%, акций Компании Б 12,4% и акций Компании В 12,9%.

_А = 0,25*18+0,5*12+0,25*3 = 11,25%

_Б = 0,3*22+0,45*14+0,25*(-2) = 12,4%

_В = 0,2*35+0,45*17+0,35*(-5) = 12,9%

Если не принимать во внимание прочие факторы (например, риск), то в портфель инвестора целесообразно включить акции Компании В, поскольку они характеризуются самой высокой ожидаемой доходностью.

Пример 2. Финансовому аналитику необходимо оценить ожидаемую доходность акций на основании данных об их исторической доходности за последние 7 недель, которые представлены в таблице.

Поскольку аналитику известна только историческая доходность акций, необходимо воспользоваться второй из приведенных выше формул.

_А = (-2,3+7+4,1-3,4+6,2+4,5+1,8)/7 = 2,56%

_Б = (4,1-5,7+2,4+4,8-1,2+1,1+0,3)/7 = 0,83%

_В = 0,2*35+0,45*17+0,35*(-5) = 0,64%

Раздел III. Основы портфельного инвестирования

Тема 8. Теория портфельного инвестирования

8.1. Необходимость формирования портфелей ценных бумаг

8.2. Ожидаемая доходность актива и портфеля

8.3. Ожидаемый риск актива и портфеля

8. 4. Риск портфеля, состоящего из двух активов

8.5. Риск портфеля, состоящего из нескольких активов

8.6. Эффективный набор портфелей

8.7. Портфель, состоящий из актива без риска и рискованного актива.

Кредитный и заёмный портфели

Термины

1. Портфель – это набор финансовых активов, которыми располагает инвестор.

2. Цель формирования портфеля – состоит в стремлении получить требуемый уровень ожидаемой доходности при более низком значении ожидаемого риска.

3. Ожидаемая доходность портфеля оценивается как среднеарифметическая взвешенная доходностей входящих в него активов.

4. Риск актива (портфеля) определяется показателями стандартного отклонения или дисперсии его доходности.

5. Риск портфеля зависит от корреляции доходностей входящих в него активов.

6. Доминирующий портфель – это портфель, который имеет самый высокий уровень доходности для данного уровня риска или наименьшее значение риска для данного значения доходности.

7. Эффективный набор портфелей – это набор доминирующих портфелей. Его также называют эффективной границей.

8. Кредитным портфелемназывают портфель, состоящий из рискованного актива и актива без риска.

9. Заёмный портфель– это портфель, который формируется вкладчиком за счёт средств займа, инвестируемого в рискованный актив.

8.1. Необходимость формирования портфелей ценных бумаг

В зависимости от объектов вложения капитала выделяют реальные и финансовые инвестиции. Если инвестор осуществляет реальные инвестиции, т. е. создаёт какое-либо предприятие или приобретает контрольный пакет акций акционерного общества, то его непосредственной задачей является обеспечение эффективной работы предприятия, так как от этого будет зависеть его прибыль.

Однако имеется большое количество инвесторов как индивидуальных (граждан), так и институциональных (паевые и пенсионные фонды, страховые компании и др.), которые не создают собственных предприятий, не имеют контрольных пакетов акций, а вкладывают свои средства в ценные бумаги (акции, облигации, производные финансовые инструменты), а также на банковские счета и вклады. Доходность и надёжность таких вложений не зависит от деятельности самого инвестора, поэтому инвестор должен самым тщательным образом подходить к отбору таких финансовых инструментов с учётом их доходности и степени риска.

Для достижения поставленных целей инвесторы обычно прибегают к дифференциации своих вложений, т. е. формируют инвестиционный портфель.

Инвестиционный портфель – это набор инвестиционных инструментов, которые служат достижению поставленных целей. Распределяя свои вложения по различным направлениям, инвестор может достичь более высокого уровня доходности своих вложений либо снизить степень их риска. Характерной особенностью портфеля является то, что риск портфеля может быть значительно меньше, чем риск отдельных инвестиционных инструментов, входящих в состав портфеля.

Главная цель формирования портфеля состоит в стремлении получить требуемыйуровень ожидаемой доходности при более низком уровне ожидаемого риска. Данная цель достигается,

во-первых, за счёт диверсификации портфеля, т. е. распределения средств инвестора между различными активами, и;

во-вторых, тщательного подбора финансовых инструментов.

В теории и практике управления портфелем существуют два подхода: традиционный и современный.

Традиционный подход основывается на фундаментальном и техническом анализе. Он делает акцент на широкую диверсификацию ценных бумаг по отраслям. В основном приобретаются бумаги известных компаний, имеющих хорошие производственные и финансовые показатели. Кроме того, учитывается их более высокая ликвидность, возможность приобретать и продавать в больших количествах и экономить на комиссионных.

Развитие широкого и эффективного рынка, статистической базы, а также быстрый прогресс в области вычислительной техники привели к возникновению современной теории и практики управления портфелем финансовых инструментов. Она основана на использовании статистических и математических методов подбора финансовых инструментов в портфель, а также на ряде новых концептуальных подходов.

Главными параметрами при управлении портфелем, которые необходимо определить менеджеру, являются его ожидаемая доходность и риск. Формируя портфель, менеджер не может точно определить будущую динамику его доходности и риска. Поэтому свой инвестиционный выбор он строит на ожидаемых значениях доходности и риска. Данные величины оцениваются, в первую очередь, на основе статистических отчётов за предыдущие периоды времени. Поскольку будущее вряд ли повторит прошлое со стопроцентной вероятностью, то полученные оценки менеджер может корректировать согласно своим ожиданиям развития будущей конъюнктуры.

В качестве инвестиционных инструментов могут выступать ценные бумаги, недвижимость, драгоценные металлы и камни, антиквариат, предметы коллекционирования. Однако следует иметь в виду, что имущественные вложения имеют свою специфику; Так, вложения в недвижимость являются нередко значительными по размеру и могут оказаться довольно рисковыми из-за падения цен на недвижимость. Кроме того, у инвестора могут возникнуть затруднения в поиске покупателя в случае продажи недвижимости. Поэтому инвестиции в недвижимость, вероятно, следует рассматривать как особый вид вложений, а не как одну из составляющих инвестиционного портфеля.

Ожидаемая доходность актива и портфеля

При наличии достаточного объёма статистических данных ожидаемая доходность актива принимается равной средней доходности.

В условиях неопределённости менеджер полагает, что рискованный актив, например акция, может принести ему различные результаты, о которых в момент формирования портфеля можно судить только с некоторой долей вероятности, как представлено в табл. 8.1.

Таблица 8.1. Доходность акции с учётом вероятности

В сумме все возможные варианты событий должны составлять 100% вероятности, как и показано в табл. 8.1. Ожидаемая доходность актива определяется как среднеарифметическая взвешенная, где весами выступают вероятности каждого исхода события.

В нашем случае ожидаемая доходность актива равна:

10% ∙ 0,3 + 13% ∙ 0,3 + 18% ∙ 0,2 + 24% ∙ 0,2 = 15%.

(В формуле ожидаемой доходности значения вероятности берут в десятичных величинах, и соответственно вероятность всех возможных вариантов событий равна единице.)

Запишем формулу определения ожидаемой доходности актива в общем виде:

E(r) =

где: Е(r) — ожидаемая доходность актива;

E(r_i) — ожидаемая доходность актива в i-м случае;

π_i — вероятность получения доходности в i-м случае.

Портфель, формируемый инвестором, состоит из нескольких активов, каждый из которых обладает своей ожидаемой доходностью. Ожидаемая доходность портфеля определяется как средневзвешенная ожидаемая доходность входящих в него активов, а именно:

где: Е(r_p) — ожидаемая доходность портфеля;

Е(r₁); Е(r₂); Е(r_n) – ожидаемая доходность соответственно первого, второго и n-го активов;

d₁; d₂; d_n – удельный вес в портфеле первого, второго и n-го активов.

Запишем формулу (8.2) в более компактном виде, воспользовавшись знаком суммы, тогда: (8.3)

Удельный вес актива в портфеле рассчитывается как отношение его стоимости к стоимости всего портфеля или:

d_i = (8.4)

где: di – удельный вес i-го актива;

Р_p – стоимость портфеля.

Сумма всех удельных весов, входящих в портфель активов, всегда равна единице.

Пример 8.1.

Портфель состоит из двух активов А и В. Е(r_a) = 15%, Е(r_B) = 10%.

Стоимость актива А – 300 тыс. руб., актива В – 700 тыс. руб. Необходимо определить ожидаемую доходность портфеля.

Стоимость портфеля равна: 300 тыс.+ 700 тыс. =1000 тыс. руб.

Удельные веса активов равны:

d₁ = d₂ =

Для определения ожидаемой доходности портфеля на основе ожидаемой доходности активов воспользуемся формулой 8.3:

Ответ:доходность портфеля составит 11,5%.

При оценке связи между показателями доходности ценных бумаг различных эмитентов предполагают, что эта связь моделируется с помощью линейной однофакторной зависимости. Данные о доходности одного из эмитентов будем называть «показатель» и обозначим его Y_i , а данные другого эмитента будем называть «фактор» и обозначим его Х_i.

Простейшей мерой тесноты связи между показателем и фактором является функция S , которая используется в методе наименьших квадратов для получения статистических коэффициентов уравнения регрессии а₀ и a₁. Чем «плотнее» точки, образованные парами наблюдений у_i и x_i лежат в районе линии регрессии, тем ближе связь между показателем Y и фактором X к функциональной (рис.1). Поскольку линия регрессии как бы вписывается в
«облако» точек, сумма квадратов остатков е_i 2 =(у_i – y_ip) 2 будет тем
меньшей, чем ближе статистическая связь к функциональной.

Рис. 1. Остатки однофакторной регрессии

Для проверки наличия корреляции при парной связи используется коэффициент ковариации (корреляционный момент) К_ух, который вычисляется по формуле

=

Если между Y и X связь отсутствует, то К_yx = 0; если связь есть,
то Кух ≠ 0. Проиллюстрируем данное утверждение на примере. Найдём коэффициенты ковариации (корреляционные моменты) для следующих пар наблюдений (рис.2):

первый случай – (1,1); (5,1); (5,5); (1,5);

второй случай – (1,1); (2,2); (3,3); (4,4); (5,5).

Рис.2. Корреляция между Y и X

а – отсутствие корреляции; б – полная корреляция

В первом случае очевидно отсутствие корреляционной связи между Y и X, во втором – связь носит функциональный характер.

В первом случае = = 3; = = 3;

=

Во втором случае = = 3; = = 3;

=

Таким образом, анализ очевидных примеров показал справедливость утверждения о том, что при отсутствии связи (первый случай) К = 0, при функциональной связи К_ух ≠ 0.

Поскольку размерность коэффициента ковариации (корреляционного момента) зависит от размерности величин У и X, для оценки тесноты линейной связи используется безразмерная величина, называемая коэффициентом
парной корреляции (r_ух) и представляющая собой отношение корреляционного момента K_vx к произведению средних квадратических отклонений показателя и фактора σ_у и σ_x: = .

В первом случае = = 2;

= = 2.

Тогда: = .

Во втором случае также одинаковы и равны:

= .

Следовательно, = .

Если рассмотреть функциональную убывающую связь пар наблюдений (5,1); (4,2); (3,3); (2,4); (1,5), то К_ух = -2, a r_yx = -1.

Полученные результаты позволяют сделать два вывода:

1) коэффициент парной корреляции изменяется в пределах от -1 (при функциональной убывающей связи) до +1 (при функциональной возрастающей связи);

2) коэффициент парной корреляции равен нулю при отсутствии
линейной связи между У и X.

Коэффициент парной корреляции является мерой приближения к линейной функциональной связи. Поэтому, если между У и X имеется функциональная связь, но она имеет нелинейный характер, то r_ух не будет равным единице.

Дисперсия определяется по формуле

(8.5)

где: σ 2 — дисперсия доходности актива;

n — число периодов наблюдения;

r – средняя доходность актива; она определяется как средняя арифметическая

доходностей актива за периоды наблюдения, а именно:

(8.6)

где: ri — доходность актива в i-м периоде.

Стандартное отклонение определяется как квадратный корень из дисперсии σ = (8.7)

где: σ— стандартное отклонение доходности актива.

Пример 8.2.

Допустим, что доходность актива в каждом году за четыре года составила следующие значения:

1-й год – 20%. 2-й год – 25%, 3-й год – 18%, 4-й год – 21 %.

1-й шаг.Определяем среднюю доходность актива за период.

=

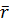
2-й шаг. Определяем отклонение величины доходности в каждом периоде от её среднего значения.

3-й шаг. Возводим в квадрат полученные отклонения и суммируем их

4-й шаг.Определяем дисперсию.

(Если имеется небольшое число наблюдений, как в нашем примере, то по правилам статистики в формуле определения дисперсии (8.5) в знаменателе вместо п — 1 берут просто значение п. )

5-й шаг. Определяем стандартное отклонение.

= 2,55%

Стандартное отклонение говорит о величине и вероятности отклонения доходности актива от её средней величины за определённый период времени. В нашем примере мы получили отклонение доходности актива за год, равное 2, 55%.

Доходность актива в том или ином году – это случайная величина. Массовые случайные процессы подчиняются закону нормального распределения. Поэтому с вероятностью 68,3% можно ожидать, что через год доходность актива будет лежать в пределах одного стандартного отклонения от средней доходности, т. е. в диапазоне 21% ± 2,55%. С вероятностью 95, 5% этот диапазон составит два стандартных отклонения, т. е. 21% ± 2 х 2,55%; и с вероятностью 99, 7% диапазон составит три стандартных отклонения, то есть 21% ± 3 х 2,55%.

Поскольку доходность актива – случайная величина, которая зависит от различных факторов, то остаётся 0,3% вероятности, что она выйдет за рамки трёх стандартных отклонений, т. е. может, как упасть до нуля, так и вырасти до очень большой величины.

Рис.8.1. Нормальное распределение доходности актива

График нормального распределения представлен на рис.8.1. Чем больше стандартное отклонение доходности актива, тем больше его риск. Например, два актива имеют одинаковую ожидаемую доходность, которая равна 50%. Однако стандартное отклонение первого актива составляет 5%, а второго – 10%. Это говорит о том, что второй актив рискованнее первого, так как существует 68,3% вероятности, что через год доходность первого актива может составить от 45% до 55%, а второго – от 40% до 60% и т. д.